大家的朋友圈有没有被
一群“羊”刷屏呢?

近日
一款名叫“羊了个羊”的小游戏走红网络

由于太火,服务器2天崩了3次
很多玩家惊呼:
我只是睡前玩一玩
没想到给我整失眠了!
“羊了个羊”的玩法非常简单
和我们之前玩的消消乐一样
三个一样的花色进入卡槽即可消除
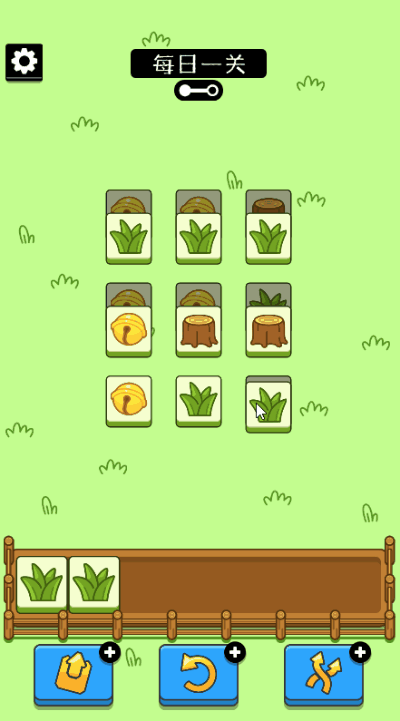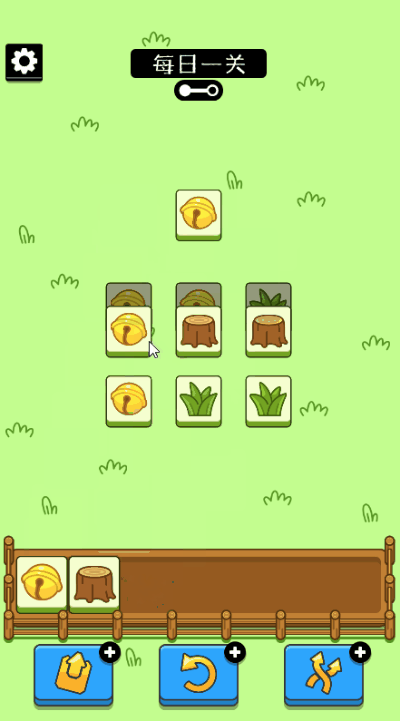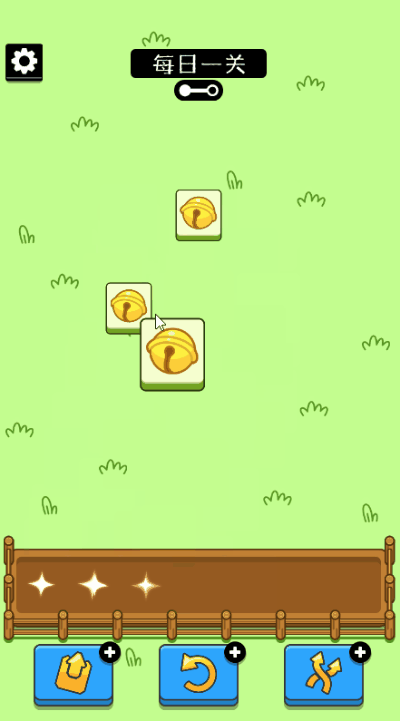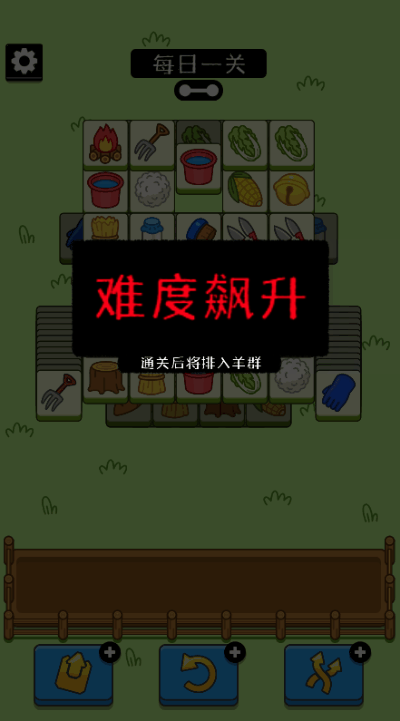
整个游戏分两关
第一关确实容易,号称“平地级别难度”
让玩家信心满满

第二关难度陡增,人称“宇宙级难度”
把玩家直接干蒙圈
“羊了个羊”的官方通关率为0.1%
但通过大量玩家实践发现
有些花色搭配根本就是“死局”
通关概率几乎为0
即使是这样
玩家们仍然愈挫愈勇、欲罢不能!

人人都想成为那个0.1%的天选之子
然而
小概率事件怎么会随随便便出现呢!

与其被“羊了个羊”这个“时间刺客”
浪费我们的生命
倒不如跟着小编
学点概率的相关知识吧~



概率论是研究随机现象数量规律的数学分支,是一门研究事情发生的可能性的学问。

概率论不仅在科学研究、经济管理、技术开发中发挥着重要作用,同时也在我们日常生活的点点滴滴中有所体现,对我们的生活有着巨大的影响。比如在理财管理、交通建设、天气预测、疾病防控等诸多领域,概率论都有着重要的应用。


抽签原理来自全概率公式,是指抽签的顺序和中签的概率无关。例如,十万张彩票如果只有10个特等奖, 则被十万个人抽取, 无论抽取的次序如何, 每个人的中奖概率都是十万分之十, 即万分之一。


生日悖论是指在不少于 23 个人中至少有两人生日相同的概率大于 50%。例如在一个 30 人的小学班级中,存在两人生日相同的概率为70%。对于 60 人的大班,这种概率要大于 99%。

三门问题亦称蒙提霍尔悖论。来源于美国的电视游戏节目。参赛者会看见三扇关闭了的门,其中一扇的后面有一辆汽车,选中后面有车的那扇门可赢得该汽车,另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门,但未去开启它的时候,节目主持人开启剩下两扇门的其中一扇,露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是:换另一扇门是否会增加参赛者赢得汽车的机率。如果严格按照上述的条件,那么答案是会。不换门的话,赢得汽车的几率是1/3。换门的话,赢得汽车的几率是2/3。

明明不同事件发生的概率各不相同,为什么我们理应预计到它们会出现?著名统计学家大卫·汉德给出了答案,他将不同的概率原理合并成统一的解释——奇迹法则:

一件事可能出现的结果,其中之一必会发生;

只要机会足够多,任何奇事情都可能出现;

通过事后再选择,可以随心所欲的人为“提升”一件事发生的概率;

环境和条件的细微改变也会导致一件事发生概率的改变;

如果出现的事件足够相似,就可以被视为相同的事件。
小编提醒
为了让我们的生活越来越好
多学概率
少玩“羊”

原标题:《沉迷“羊了个羊”无法自拔?概率论带你出坑》